Moyenne, variance et écart-type

Des outils d’analyse comme Google Analytics ou SiteCatalyst permettent de rapporter toutes sortes de moyennes et de taux. Il peut cependant être utile d’explorer ce qui se cache derrière ces moyennes à l’aide de la déviation standard (l’écart-type).

Le problème de la moyenne

Prenons 3 séries de chiffres représentant le nombre de conversions pour un processus d’achat en ligne dans la dernière semaine:

1.  666, 666,666, 666, 666, 666, 666
2. 507, 693, 750, 644, 576, 680, 812
3. 302, 1194, 500, 107, 1542, 599, 418

Si on calcule la moyenne pour chaque série, on obtient 666. 3 fois 666.  Mais est-ce que le 666 de la série 1 signifie la même chose que le « 666 » de la série 2 ou de la série 3?

La déviation à la rescousse

La déviation est le fait de dévier, de s’écarter.

Le problème est que pour nos 3 séries de chiffres précédentes la somme de toutes les écarts par rapport à la moyenne est égale à 0. C’est d’ailleurs, selon nos amis les statisticiens, une des propriétés constituantes de la moyenne.

1.  0 + 0 + 0 + 0 + 0 + 0 = 0
2. -159 + 27 + 84 -22 -90 + 14 +146= 0
3. -364 +528 -166 -559 + 876 -67 – 248 = 0

La variance à la rescousse

La variance est très utile pour éviter d’avoir une déviation qui est nulle. Elle sert à mesurer le niveau de dispersion d’une série de nombres par rapport à la moyenne. Elle consiste en la moyenne de la somme du carré des déviations d’un groupe de nombres déterminés. Sa formule est très jolie :

Formule de la variance

Dans le cas des écarts qui nous intéressent, on obtient:

1. (0+0+0+0+0+0)/6 = 0
2. (25281 + 729 + 7056 + 484 + 8100 + 196 + 21316)/7 = 9023,14286
3. (132496+278784+27556+312481+767376+4489+61504)/7 = 226383,714

VAR.P. houlala

Heureusement, la fonction statistique VAR.P de Excel nous permet de calculer la variance en deux temps trois mouvements.

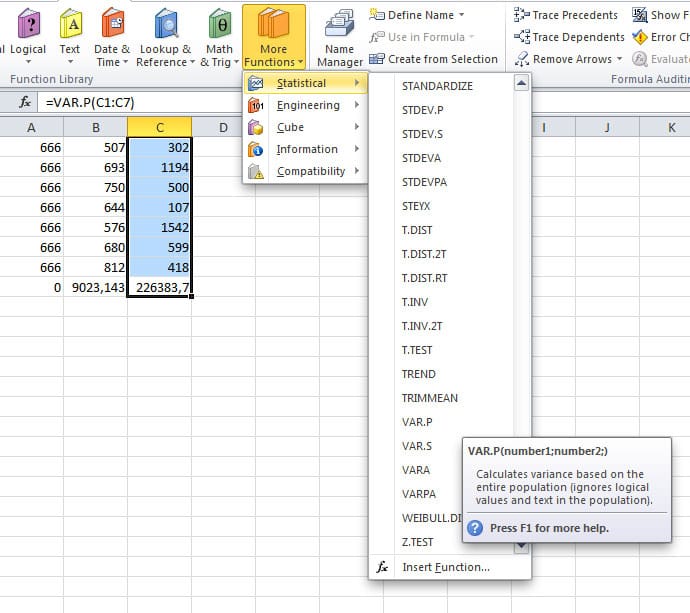Calculer la variance dans Excel

L’écart-type à la rescousse

Tout ça est bien beau, mais l’unité de mesure de la variance est différente de l’unité de mesure de notre série de nombres initiale.  Si par exemple, nos conversions sont en dollars, nous nous retrouverons avec une variance en dollars au carré.

L’écart-type (déviation standard) permet de contourner ce problème. Elle consiste tout simplement en la racine carrée de la variance.

1. racine carré (0) = 0
2. racine carrée (9023,14286) = 94,9902251
3. racine carrées (226383,714) = 475,797976

STDEV.P mon kiki

Heureusement, encore une fois, la fonction statistique STDEVP d’Excel nous permet de calculer la déviation standard presque automatiquement.

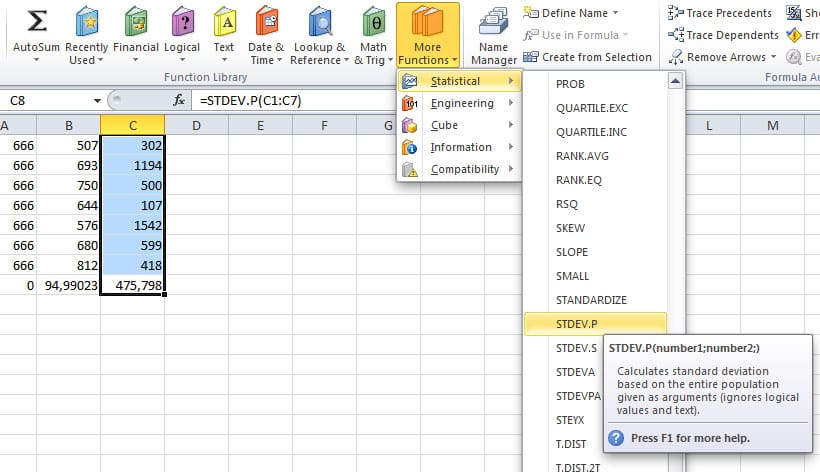Calculer la variation standard dans Excel

Dispertion des données

Une moyenne c’est intéressant, peut-être même réconfortant. Mais le niveau de dispersion des données – l’écart-type –  par rapport à la moyenne peut être très déstabilisant, au point de devenir monstrueux, anormal.

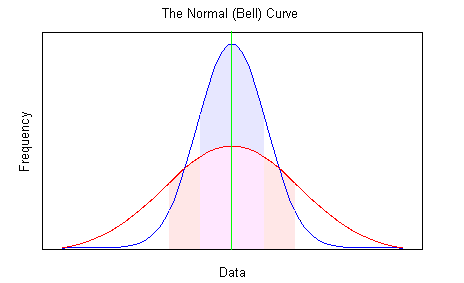Exemples de dispersions par rapport à  la moyenne

Plus l’écart est élevée, plus la dispersion des données est élevé et plus un processus mesuré est instable.

Exemple de processus instable

Plus l’écart est faible, moins la dispersion des données est élevé et plus un processus mesuré est stable.

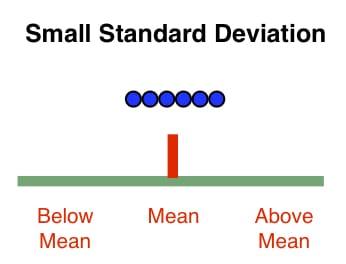Exemple de processus stable

Au final, plus un processus mesuré est stable et plus il y a de probabilités d’obtenir des résultats près de la moyenne dans le futur. Et de faire des prédictions fiables.

Reste maintenant à mieux comprendre :

1. comment se distribuent les données dispersées autour de la moyenne;
2. ce qui se passe quand un résultat est plus grand ou plus petit que l’écart positif ou négatif entre la moyenne et l’écart-type.

La photo provient de http://www.deviation-standard.com/